Con lắc lò xo – có lẽ đây là cụm từ đã khiến không ít học sinh “toát mồ hôi” mỗi khi đối diện trong các kì thi quan trọng. Không chỉ là nền tảng cơ bản của chương Dao động cơ trong Vật lý 12, mà các bài tập con lắc lò xo còn được biến tấu vô cùng đa dạng, từ việc tìm chu kỳ, năng lượng cho đến những bài toán thời gian, quãng đường hóc búa. Đừng lo lắng! Với kinh nghiệm xây dựng và hiệu đính tài liệu học thuật cho “Cung ứng giáo viên”, tôi hiểu rõ những điểm nghẽn mà học sinh thường gặp phải. Bài viết này không chỉ cung cấp công thức, mà còn là một lộ trình tư duy chuyên nghiệp, giúp bạn “gỡ rối” triệt để mọi dạng bài về con lắc lò xo.
Giống như việc chuẩn bị kỹ lưỡng cho một kì thi quan trọng như đề thi giữa kì 1 tiếng anh 7 global success cần có phương pháp, việc chinh phục con lắc lò xo cũng đòi hỏi bạn phải nắm vững bản chất, phân loại đúng dạng và áp dụng chiến thuật phù hợp. Hãy cùng nhau khám phá nhé!
Tổng Quan: Nắm Chắc “Linh Hồn” Của Con Lắc Lò Xo
Bản chất của con lắc lò xo là một hệ dao động điều hòa (DĐĐH), nơi sự biến thiên của động năng và thế năng luôn tuân theo một quy luật chặt chẽ. Để giải quyết các bài tập con lắc lò xo một cách trơn tru, bạn cần khắc cốt ghi tâm hai yếu tố nền tảng sau:
1. “Chìa Khóa Vàng” – Các Công Thức Cốt Lõi
Mọi vấn đề về con lắc lò xo đều quy về việc xác định ba thông số chính: Tần số góc ($omega$), Chu kỳ ($T$) và Tần số ($f$).
-
Tần số góc ($omega$):
$$omega = sqrt{frac{k}{m}}$$
Trong đó: $k$ là độ cứng lò xo (N/m), $m$ là khối lượng vật nặng (kg). Đây là công thức quan trọng nhất, nó định nghĩa tốc độ “lắc” của con lắc. -
Chu kỳ ($T$):
$$T = frac{2pi}{omega} = 2pisqrt{frac{m}{k}}$$
Chu kỳ là thời gian để vật thực hiện được một dao động toàn phần. -
Lực kéo về ($F_{kv}$):
$$F_{kv} = -kx$$
Lực này luôn hướng về vị trí cân bằng ($x=0$), chính là nguyên nhân tạo ra dao động điều hòa.
Trích dẫn từ Chuyên gia: “Thành công của việc giải bài tập con lắc lò xo không nằm ở việc nhớ công thức, mà ở việc hiểu rõ: Lực kéo về chính là động lực tạo ra Dao động điều hòa. Bất kỳ sự thay đổi nào về khối lượng hay độ cứng đều phải được xem xét thông qua $omega$.” – TS. Nguyễn Anh Tuấn, Chuyên gia Vật lý ứng dụng.
Hình ảnh minh họa con lắc lò xo ngang và các thông số cơ bản giúp giải bài tập con lắc lò xo
2. Sự Khác Biệt Giữa Con Lắc Ngang và Thẳng Đứng
- Con lắc ngang: Vị trí cân bằng (VTCB) là vị trí lò xo không biến dạng ($x=0$).
- Con lắc thẳng đứng: Do ảnh hưởng của trọng lực, VTCB nằm dưới vị trí lò xo không biến dạng một đoạn $Delta l_0$.
$$Delta l_0 = frac{mg}{k}$$
Khi làm bài tập con lắc lò xo thẳng đứng, bạn phải luôn nhớ quy chiếu mọi thứ về VTCB mới.
Phân Loại Các Dạng Bài Tập Con Lắc Lò Xo “Gây Rối” Nhất
Dạng 1: Viết Phương Trình Dao Động (Xác Định A, $omega$, $phi$)
Đây là dạng bài cơ bản nhất nhưng lại đòi hỏi sự tổng hợp.
Phương pháp giải nhanh:
- Tính Tần số góc ($omega$): Luôn là bước đầu tiên bằng công thức $omega = sqrt{k/m}$.
- Tìm Biên độ ($A$): Thường dựa vào Định luật bảo toàn năng lượng hoặc các dữ kiện về vận tốc và li độ: $A = sqrt{x^2 + frac{v^2}{omega^2}}$.
- Xác định Pha ban đầu ($phi$): Dựa vào điều kiện ban đầu ($t=0$):
- $x_0 = Acosphi$
- $v_0 = -omega Asinphi$
- Quan sát xem vật đang chuyển động theo chiều dương hay chiều âm để chọn $phi$ cho chính xác.
Dạng 2: Bài Toán Năng Lượng (Thế năng, Động năng, Cơ năng)
Năng lượng là một khía cạnh cốt lõi. Nắm vững nó giúp giải quyết các bài toán liên quan đến vận tốc cực đại, lực cực đại…
- Cơ năng ($W$): Luôn được bảo toàn và bằng tổng động năng ($W_d$) và thế năng ($W_t$).
$$W = W_t + W_d = frac{1}{2}k A^2 = frac{1}{2}m omega^2 A^2$$
(Thường nên tính $W$ qua biên độ $A$ vì nó là hằng số.) - Thế năng ($W_t$): Năng lượng do biến dạng lò xo.
$$W_t = frac{1}{2} k x^2$$ - Động năng ($W_d$): Năng lượng do chuyển động.
$$W_d = frac{1}{2} m v^2$$
Mối liên hệ quan trọng:
Các bài tập nâng cao thường hỏi về vị trí mà $W_d = n cdot W_t$.
Áp dụng: $W = W_d + W_t = n W_t + W_t = (n+1) W_t$.
$$Rightarrow frac{1}{2} k A^2 = (n+1) cdot frac{1}{2} k x^2 Rightarrow x = pm frac{A}{sqrt{n+1}}$$
Đây là công thức “tủ” giúp bạn giải nhanh các bài toán này.
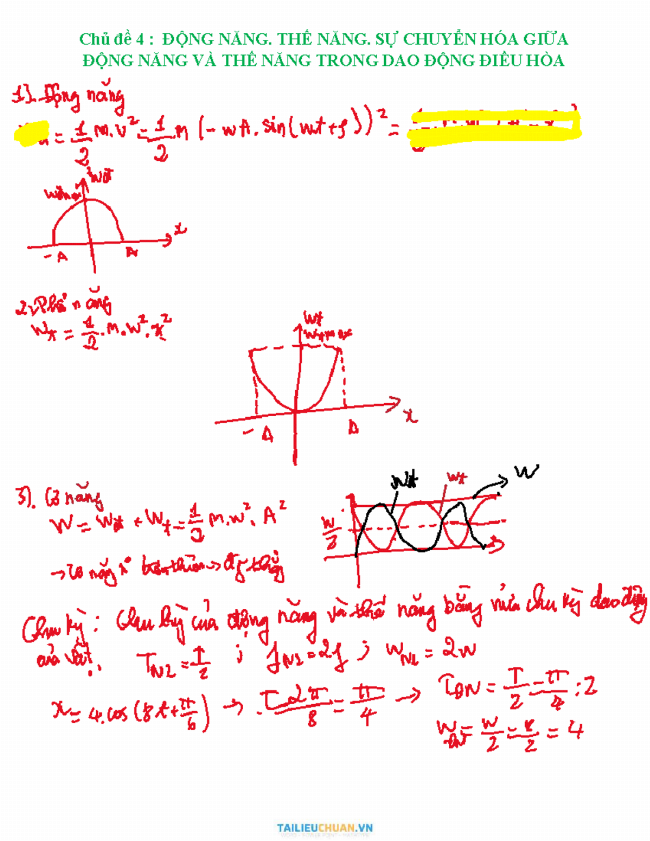Đồ thị biểu diễn sự biến thiên và chuyển hóa của Động năng và Thế năng trong bài tập con lắc lò xo
Dạng 3: Con Lắc Lò Xo Thẳng Đứng và Lực Đàn Hồi
Đây là dạng dễ nhầm lẫn nhất vì phải phân biệt giữa Lực kéo về và Lực đàn hồi.
- Lực kéo về ($F_{kv}$): Hướng về VTCB ($O$). $F_{kv} = -k x$ (với $x$ là li độ so với $O$).
- Lực đàn hồi ($F_{đh}$): Hướng về vị trí lò xo không biến dạng ($O’$). $F_{đh} = -k Delta l$ (với $Delta l$ là độ biến dạng so với $O’$).
Yếu tố then chốt cần tìm:
- Độ giãn tại VTCB ($Delta l_0$): $Delta l_0 = mg/k$.
- Độ giãn/nén cực đại:
- Độ giãn Max: $Delta l_{max} = Delta l_0 + A$
- Độ nén Max: $Delta l_{min} = | Delta l_0 – A |$ (Nếu $A le Delta l0$ thì $Delta l{min}=0$).
Các bài tập con lắc lò xo thẳng đứng thường xoay quanh việc tính lực đàn hồi cực đại/cực tiểu hoặc thời gian lò xo bị nén/giãn trong một chu kỳ.
Dạng 4: Bài Toán về Thời Gian và Quãng Đường
Dạng này yêu cầu vận dụng linh hoạt Phương pháp Vòng tròn Lượng giác (Quay Vector). Đây là kỹ năng phải có nếu bạn muốn đạt điểm cao.
Chiến thuật:
- Vẽ Vòng tròn: Trục hoành là trục li độ $x$.
- Xác định các vị trí đặc biệt: $A$, $-A$, $A/2$, $Asqrt{2}/2$, $Asqrt{3}/2$, và VTCB $O$.
- Biểu diễn trạng thái ban đầu: Dùng pha ban đầu $phi$ để xác định điểm $M_0$ trên vòng tròn.
- Tính thời gian: Khoảng thời gian vật đi từ vị trí $x_1$ đến $x_2$ tương ứng với góc quét $Deltaalpha$ của vector quay.
$$t = frac{Deltaalpha}{omega}$$
Lưu ý: Việc tính toán thời gian này rất quan trọng, tương tự như khi ta nghiên cứu về dao động tắt dần là một dao động có, hiểu được quy luật biến thiên theo thời gian là chìa khóa để giải quyết vấn đề.
Bí Quyết “Gỡ Rối” Bài Tập Con Lắc Lò Xo Hiệu Quả (Kinh nghiệm chuyên gia)
Giải bài tập con lắc lò xo không chỉ là thay số vào công thức, mà là một nghệ thuật tư duy vật lý.
1. Phân Biệt “Gốc” Tọa Độ: VTCB hay Vị Trí Lò Xo Tự Nhiên?
Đây là lỗi sai phổ biến nhất. Luôn tự hỏi: “Li độ ($x$) này đang được tính so với đâu?”.
- $x$ (trong $x = Acos(omega t + phi)$) là li độ so với VTCB.
- $Delta l$ (trong $F_{đh} = k Delta l$) là độ biến dạng so với vị trí lò xo không biến dạng.
Việc phân biệt rõ ràng hai gốc tọa độ này sẽ giúp bạn không bao giờ nhầm lẫn giữa Lực kéo về và Lực đàn hồi, đặc biệt trong con lắc thẳng đứng.
2. Chuẩn Hóa Đơn Vị Trước Khi Bấm Máy
Đừng để mất điểm oan vì sai đơn vị. Đây là quy tắc bất di bất dịch:
| Đại lượng | Đơn vị chuẩn (SI) | Cần đổi |
|---|---|---|
| Khối lượng ($m$) | kg | g $rightarrow$ kg |
| Độ cứng ($k$) | N/m | N/cm $rightarrow$ N/m |
| Li độ, Biên độ ($x, A$) | m | cm $rightarrow$ m |
Giữ thói quen này, bạn sẽ tránh được 90% lỗi sai do tính toán. Việc luyện tập kiến thức chuyên môn thường xuyên, giống như ôn luyện đề thi tiếng anh giữa kì 1 lớp 8 cần sự chính xác, sẽ giúp bạn xây dựng phản xạ đúng.
3. Tận Dụng Phương Pháp Đồ Thị và Đạo Hàm
Khi gặp các bài toán khó về thời gian hoặc vận tốc tức thời, đừng ngần ngại phác thảo đồ thị li độ – thời gian ($x-t$) hoặc vòng tròn lượng giác.
- Vòng tròn Lượng giác: Giúp “trực quan hóa” thời gian và quãng đường một cách nhanh chóng.
- Đạo hàm/Nguyên hàm: Nắm vững mối quan hệ đạo hàm: $x xrightarrow{text{đạo hàm}} v xrightarrow{text{đạo hàm}} a$. Điều này cực kỳ quan trọng khi bạn cần chuyển đổi giữa li độ, vận tốc và gia tốc.
Hướng Dẫn Tự Luyện Tập Để Chinh Phục Con Lắc Lò Xo
Checklist Ôn Tập Hiệu Quả
- Nắm vững 3 Công Thức Gốc: $omega$, $T$, $W$.
- Phân loại: Con lắc ngang và Thẳng đứng. (Xác định $Delta l_0$).
- Luyện tập chuyên sâu Dạng 4: Thực hành 10 bài toán về Thời gian và Quãng đường bằng Phương pháp Vòng tròn.
- Tập trung vào sự biến thiên: Giải ít nhất 5 bài toán về Năng lượng (ví dụ: tìm $x$ khi $W_d=3W_t$).
Câu Hỏi Thường Gặp (FAQ) Về Bài Tập Con Lắc Lò Xo
Q1: Khi nào thì lực đàn hồi bằng không trong con lắc lò xo thẳng đứng?
A: Lực đàn hồi ($F_{đh} = k cdot Delta l$) bằng không khi lò xo trở về vị trí không biến dạng (tức là $Delta l = 0$). Vị trí này là $O’$, nằm trên VTCB $O$ một đoạn $Delta l_0$.
Q2: Quãng đường vật đi được trong một chu kỳ là bao nhiêu?
A: Quãng đường vật đi được trong một chu kỳ ($T$) luôn luôn là $4A$ (Bốn lần Biên độ), bất kể biên độ đó lớn hay nhỏ, miễn là vật thực hiện Dao động điều hòa.
Q3: Tốc độ cực đại của vật được tính như thế nào?
A: Tốc độ cực đại ($V{max}$) luôn xảy ra tại Vị trí Cân Bằng (VTCB) và được tính bằng công thức $V{max} = omega A$.
Q4: Cơ năng của con lắc lò xo phụ thuộc vào yếu tố nào?
A: Cơ năng ($W$) của con lắc lò xo chỉ phụ thuộc vào Biên độ ($A$) và Độ cứng lò xo ($k$) theo công thức $W = frac{1}{2} k A^2$. Nó không phụ thuộc trực tiếp vào thời gian hay khối lượng (mặc dù $m$ ảnh hưởng đến $omega$ và $A$ có thể bị thay đổi).
Q5: Có phải mọi dao động của lò xo đều là Dao động điều hòa không?
A: Không. Để là Dao động điều hòa, dao động phải là tự do (không ma sát, không ngoại lực cưỡng bức) và vật phải tuân theo Định luật II Newton dưới tác dụng của lực kéo về. Trong thực tế, các dao động thường là dao động tắt dần là một dao động có.
Kết Luận
Chinh phục bài tập con lắc lò xo không phải là thử thách quá lớn nếu bạn trang bị cho mình một tư duy vật lý khoa học và phương pháp giải quyết vấn đề bài bản. Hãy luôn bắt đầu từ gốc rễ: $omega = sqrt{k/m}$, sau đó phân loại dạng bài và áp dụng linh hoạt các kỹ thuật như Vòng tròn Lượng giác. Việc nắm chắc lý thuyết nền và luyện tập chuyên sâu sẽ giúp bạn không còn sợ hãi trước bất kỳ biến tấu phức tạp nào của con lắc lò xo trong các kỳ thi sắp tới. Chúc các bạn học tập hiệu quả!
